14. marts er ingen regelmæssig Pi-dag i år. Matematikentusiaster overalt fejrer begivenheden som Ultimate Pi-dag, fordi datoen vil svare til de første fem cifre i pi (3.1415) snarere end bare de første tre. Denne matematiske sammenflydelse kommer ikke tilbage i et århundrede den 14. marts 2115.
Relateret indhold
- Verden er fuld af cirkler
Defineret som forholdet mellem en cirkels omkreds og dens diameter, er pi ( π ) både et transcendentalt og et irrationelt tal, hvilket betyder, at det aldrig kan skrives som forholdet mellem to hele tal, og det fortsætter på ubestemt tid uden noget gentagende mønster. Pi er ikke det eneste irrationelle tal - der er også Eulers nummer (e) og det gyldne forhold ( φ eller phi), for eksempel. Men det fortsætter med at være en kilde til fascination, fordi dens oprindelse let kan forklares, siger Mario Livio, en astrofysiker ved Space Telescope Science Institute i Maryland.
”Alle kan forstå, hvordan pi er afledt. Alle de andre numre er mere komplekse. Antallet phi involverer for eksempel en bestemt opdeling af en linje, og tallet e kræver, at du ved, hvad en logaritme er, ”siger Livio, forfatter til bogen Er Gud en matematiker?
En anden stor del af pi's appel er, at det har en uhyggelig evne til at vises i matematiske formler, hvoraf mange er vigtige for daglige processer fra billedbehandling til GPS-navigation. Her er bare en lille prøveudtagning af de ofte anvendte formler, der inkluderer pi:
Fourier Transform
Opkaldt efter den franske matematiker Jean-Baptiste Joseph Fourier, nedbryder dette matematiske værktøj et signal i dets komponentfrekvenser - snarere som hvordan en musikalsk akkord kan opdeles i dens komponentnoter. I det væsentlige er Fourier-transformationer ideelle til at behandle bølgebaserede signaler som lyd eller lys og finde mønstre. Det gør Fourier-transformationen til et grundlæggende værktøj i den moderne digitale verden.
”Det kaldes den eneste vigtigste algoritme, der nogensinde er udviklet af menneskeheden. Nu kan det være hyperbole, men måske er det ikke, ”siger Glen Whitney, grundlægger og direktør for National Museum of Mathematics i New York City. Fourier-transformationer bruges hele tiden til at rydde op i digitale billeder, til automatisk indstille popstjerner og til at finde fjerntliggende planeter, der kredser om andre stjerner. Værktøjet er også afgørende for de tale-til-tekst-funktioner, der nu er standard på smartphones. ”Når du bruger Siri eller Google Now, er et af de første skridt at tage din stemme og foretage en Fourier-transformation på det ... det viser sig at være meget lettere at genkende vokaler, når man ser på deres Fourier-transforms end når man ser på originale signaler selv, ”siger Whitney.
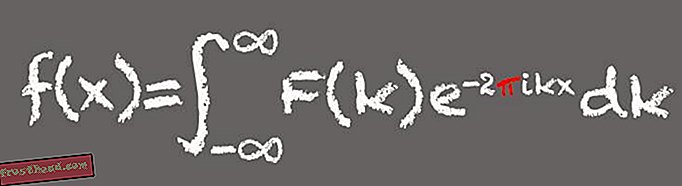(Illustration af Victoria Jaggard) Pi vises i Fourier-transformen, fordi en af komponentdelene eller udtrykket i formlen er forbundet med sinus og cosinus og vinklerne skabt af en partikel, der bevæger sig rundt i en cirkel. ”Hver gang du har en formel, der handler med cirkler eller vinkler, vil du ikke blive overrasket, når pi dukker op, ” siger Whitney.
Heisenberg usikkerhedsprincip
En af søjlerne i kvantemekanikken, Heisenbergs usikkerhedsprincip, siger, at en observatør ikke kan kende både positionen og hastigheden af en subatomisk partikel samtidig. I stedet for, jo mere præcist en partikels position kendes, desto mindre kan man vide om dens hastighed.
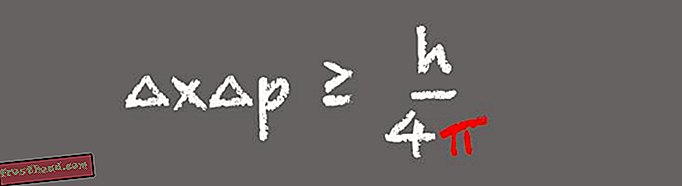(Illustration af Victoria Jaggard) Udseendet af pi i Heisenbergs usikkerhedsprincip giver mening, når man er klar over, at der i formlen, positionen og momentumet er Fourier-transformationer af hinanden, siger Whitney. Usikkerhedsprincippet er vigtigt i den moderne verden, fordi det beskriver opførsel af lyspartikler eller fotoner i fiberoptiske kommunikationssystemer. ”Hvad det fortæller os, er, at vi ikke kan kende både fotonenes position og fremdrift med ekstrem præcision. Du kan ikke designe kommunikationsprotokoller, der krænker Heisenbergs usikkerhedsprincip, fordi de ikke fungerer. ”
Stoke's Law
Stokes lov beregner den krævede kraft til at bevæge en lille kugle - det vil sige en tredimensionel cirkel - gennem en tyktflydende væske med en bestemt hastighed. Det har applikationer inden for områder, der spænder fra jordvidenskab til medicin.
(Illustration af Victoria Jaggard) "Loven handler specifikt om effekten af viskositet på en kugle i væsken, " siger Whitney, og det er sådan, pi kommer ind i spillet. Hvad angår praktisk anvendelse af Stokes lov, skal du ikke lede længere end din bil. ”I årtier var den måde, virksomhederne sørgede for, at din motorolie havde den rigtige viskositet for din bil på, at bogstaveligt talt fælde en række testsfærer i olien og måle den tid det tager dem at falde gennem væsken, ” siger Whitney. I dag involverer den mest almindelige måde at måle olieviskositet på et værktøj kaldet et kapillarrørsviskometer, ingen sfærer er nødvendige - men det rapporterer stadig resultatet i måleenheder kaldet centistoke.
Eulers formel
Opkaldt efter den schweiziske matematiker Leonard Euler samler versionen af denne formel, der inkluderer pi, nogle af de mest spændende tal i matematik ét sted:
(Illustration af Victoria Jaggard) ”Alle synes bare, at dette er utroligt. Alle disse tal, som vi betragter som specielle, vises i en smuk ligning, ”siger Livio. Selvom denne småformel kan inspirere ærefrygt hos matematikere, er ligningens mere nyttige form lidt længere:
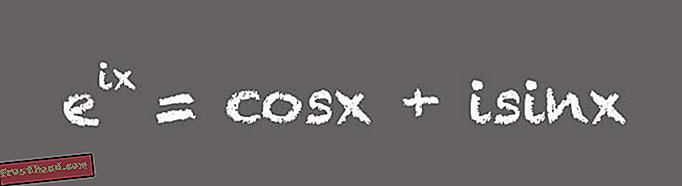(Illustration af Victoria Jaggard) Denne udpakede version af Eulers formel er et utroligt værktøj, siger Whitney. For eksempel er det vigtigt at designe elektronik, der bruger vekselstrøm eller vekselstrøm. "Eulers formel i den udvidede form betyder, at du kan bruge komplekse eller imaginære tal til at analysere og designe vekselstrømskredsløb, " siger Whitney. Det skyldes, at spændingen i et vekselstrømskredsløb er en mængde, der svinger med tiden - typisk 60 gange pr. Sekund, for eksempel i standard amerikansk elektrisk forsyning. ”Den fulde version af Eulers formel lærer, hvordan vi kan bruge komplekse tal som et praktisk kort for at modellere svingende fænomener, ” siger Whitney.
Einsteins feltligninger
Albert Einsteins feltligninger beskriver, hvordan tyngdekraft fra masse og energi skaber rumtidens krumning som en kerneelement i hans generelle relativitetsteori.
(Illustration af Victoria Jaggard) ”At beskrive, at krumning involverer geometri, og da den oprindelige definition af pi kommer fra geometri, er det udseende i denne ligning ikke så overraskende, ” siger Livio. Ud over at afsløre en grundlæggende sandhed om, hvordan universet fungerer, har generel relativitet mange praktiske anvendelser. F.eks. Ville satellitterne, der udgør det globale positioneringssystem, der bruges til navigation, håbløst være ude af synkronisering med hinanden, hvis ingeniørerne ikke tog hensyn til tidsudvidelseseffekterne, der er forudsagt af teorien.
